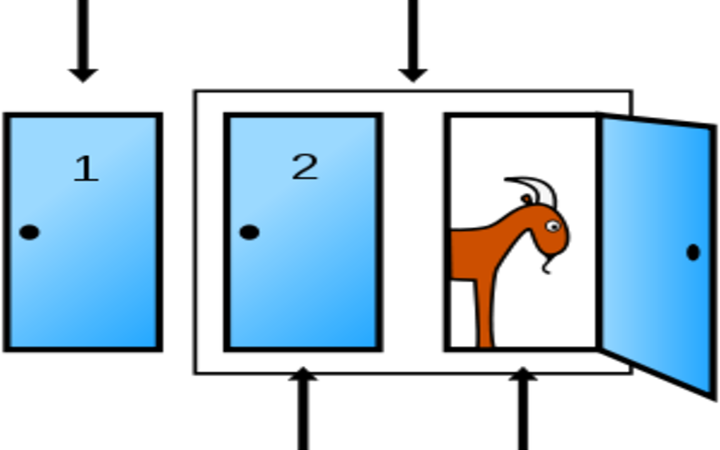
Il paradosso di Monty Hall, o problema di Monty Hall, è un famoso problema di teoria della probabilità. Prende il nome da Maurice Halprin, in arte Monty Hall, conduttore del gioco a premi statunitense “Let’s Make a Deal”, su cui il problema si basa. La soluzione, sebbene logicamente ineccepibile, è spesso controintuitiva e ha generato accesi dibattiti.
Indice dei contenuti
Le regole del gioco: tre porte e una scelta
Il gioco è semplice:
- Al concorrente vengono mostrate tre porte chiuse.
- Dietro una porta c’è un’auto (il premio), dietro le altre due ci sono delle capre.
- Il concorrente sceglie una porta, senza aprirla.
- Il conduttore, che sa cosa c’è dietro ogni porta, apre una delle due porte non scelte dal concorrente, mostrando sempre una capra.
- Il conduttore offre al concorrente la possibilità di cambiare la sua scelta iniziale con l’altra porta rimasta chiusa.
Strategie a confronto: la scelta che massimizza la vincita
Contrariamente a quanto si potrebbe pensare, la decisione se cambiare o meno la porta ha un impatto drastico sulle probabilità di vincere l’auto.
| Strategia | Probabilità di vincere l’auto |
|---|---|
| Mantenere la scelta iniziale | 1/3 (circa 33,3%) |
| Cambiare porta | 2/3 (circa 66,7%) |
Perché cambiare porta? La spiegazione dettagliata
I tre scenari possibili
Per capire il perché, analizziamo tutti i possibili scenari iniziali, assumendo di scegliere sempre la Porta 1 e di cambiare sempre scelta:
- Il giocatore sceglie la porta con la Capra 1 (probabilità 1/3):
- Il conduttore deve aprire la porta con la Capra 2.
- Cambiando porta, il giocatore vince l’auto. (Vittoria)
- Il giocatore sceglie la porta con la Capra 2 (probabilità 1/3):
- Il conduttore deve aprire la porta con la Capra 1.
- Cambiando porta, il giocatore vince l’auto. (Vittoria)
- Il giocatore sceglie la porta con l’Auto (probabilità 1/3):
- Il conduttore apre una delle due porte con le capre.
- Cambiando porta, il giocatore perde. (Sconfitta)
In due casi su tre, cambiare porta porta alla vittoria.
L’informazione chiave: la scelta del conduttore
L’azione del conduttore *non è casuale*. Egli *sa* dove si trova l’auto e *sceglie deliberatamente* di aprire una porta con una capra. Inizialmente, la probabilità di scegliere l’auto è di 1/3; di conseguenza, la probabilità che l’auto si trovi dietro *una delle altre due porte* è di 2/3. Quando il conduttore rivela una capra, i 2/3 di probabilità che l’auto fosse dietro una delle due porte non scelte *si concentrano* sull’unica porta rimasta chiusa. Cambiare significa scommettere sulla probabilità iniziale di 2/3 di aver sbagliato porta.
Il dibattito che ingannò il mondo: il caso di Marilyn vos Savant
Nel 1990, il problema divenne famoso grazie a Marilyn vos Savant, all’epoca detentrice del Guinness World Record per il quoziente intellettivo più alto. Nella sua rubrica sulla rivista “Parade”, rispose a un lettore consigliando di cambiare sempre porta. Questa affermazione scatenò un’incredibile polemica. Come riportato da testate come il New York Times, circa 10.000 lettori, tra cui centinaia di matematici e professori universitari, le scrissero per dirle che si sbagliava, sostenendo che la probabilità fosse 50/50. Vos Savant, tuttavia, non ritrattò e alla fine dimostrò, con l’aiuto di simulazioni e spiegazioni più dettagliate, la correttezza della sua soluzione basata sulla probabilità condizionata.
Il paradosso di Monty Hall dimostra l’importanza di un approccio rigoroso e non intuitivo al calcolo delle probabilità. In conclusione, la prossima volta che vi troverete di fronte a tre porte, ricordate: cambiare conviene!
Fonte immagine: Wikipedia
Articolo aggiornato il: 07/09/2025
François Villon: biografia e opere del primo poeta maledetto François Villon è una delle figure più enigmatiche e affascinanti della Scopri di più
Se si desidera optare per vacanze greche all’insegna del relax e di emozioni inedite, evitando al contempo d’essere sopraffatti da Scopri di più
La cultura cinese è una delle più antiche e affascinanti al mondo, ricca di tradizioni, riti e modi di pensare Scopri di più
Il Mito della Biga Alata, narrato da Platone nel dialogo del *Fedro*, è una delle più potenti allegorie della filosofia Scopri di più
Perché in Giappone si tolgono le scarpe: storia e galateo A chi non è capitato, guardando cartoni animati giapponesi, di Scopri di più
Le commedie di Aristofane rappresentano una pietra miliare nella storia del teatro classico. Il teatro greco, nato ad Atene, comprendeva Scopri di più
