Partiamo da 1,618, probabilmente il numero più discusso ed enigmatico del mondo. Questa costante matematica sembra celarsi dietro innumerevoli aspetti del reale, dalla botanica all’anatomia, dall’architettura all’informatica, tanto da essere considerata da alcuni come una firma del creatore stesso. Per questo motivo il numero Φ (phi) è definito il numero della proporzione divina.
Indice dei contenuti
- Caratteristiche principali della proporzione divina
- Che cos’è la sezione aurea e quanto vale
- Il legame con la successione di Fibonacci
- Storia del numero aureo: da Euclide a Pacioli
- Esempi di sezione aurea in natura
- La divina proporzione nell’arte, musica e corpo umano
- Psicologia ed estetica: il numero della bellezza?
- Domande frequenti sul rapporto aureo (FAQ)
Caratteristiche principali della proporzione divina
| Elemento chiave | Dettaglio tecnico |
|---|---|
| Simbolo matematico | Φ (Phi), in onore di Fidia. |
| Valore numerico | ≈ 1,6180339887… (Numero irrazionale). |
| Formula esatta | (1 + √5) / 2 |
| Relazione geometrica | Sezione aurea, rettangolo aureo, spirale logaritmica. |
| Applicazioni | Botanica (fillotassi), Arte, Architettura, Design, Musica. |
Che cos’è la sezione aurea e quanto vale
Il rapporto aureo, noto anche come sezione aurea o proporzione divina, è una costante matematica il cui valore approssimato è 1,6180339887… In matematica, è rappresentato dalla lettera greca Φ (phi). La sua definizione geometrica è tanto semplice quanto affascinante: due lunghezze (a e b, con a > b) sono in rapporto aureo se il rapporto tra la loro somma e la lunghezza maggiore è uguale al rapporto tra la lunghezza maggiore e quella minore.
In formula algebrica esatta, il numero corrisponde a:
Φ = (1 + √5) / 2 ≈ 1,618
Questa proporzione dà origine al rettangolo aureo, una forma considerata particolarmente equilibrata e piacevole alla vista, le cui proprietà sono state studiate sin dall’antichità.
Il legame con la successione di Fibonacci
Quando parliamo della serie di Fibonacci ci riferiamo a una sequenza di numeri in cui ognuno è dato dalla somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… e così via all’infinito. Lo scopo iniziale del matematico pisano Leonardo Fibonacci era quello di descrivere in modo teorico la crescita di una popolazione di conigli.
Ma cosa c’entra Fibonacci con il rapporto aureo Φ?
Il legame è diretto e sorprendente. Per ottenere il nostro magico numero basterà calcolare il rapporto tra due numeri consecutivi della successione. Il valore ottenuto sarà tanto più preciso e vicino a 1,618 quanto più i numeri considerati sono alti nella sequenza. Le sue infinite cifre decimali ne fanno un numero irrazionale, tra i più difficili da approssimare con un rapporto tra due numeri interi.
| Rapporto tra termini di Fibonacci | Risultato approssimato |
|---|---|
| 3 / 2 | 1,5 |
| 5 / 3 | 1,666… |
| 13 / 8 | 1,625 |
| 89 / 55 | 1,61818… |
| 144 / 89 | 1,61797… |
Storia del numero aureo: da Euclide a Pacioli
Sebbene la connessione con Fibonacci sia relativamente moderna, la sezione aurea è nota da millenni. Le prime testimonianze scritte risalgono a Euclide, che nei suoi “Elementi” intorno al 300 a.C. la definì come “proporzione media ed estrema”. Tuttavia, si ritiene che le sue proprietà fossero già conosciute da matematici greci precedenti, come i Pitagorici, che associavano il rapporto al pentagono stellato o pentagramma.
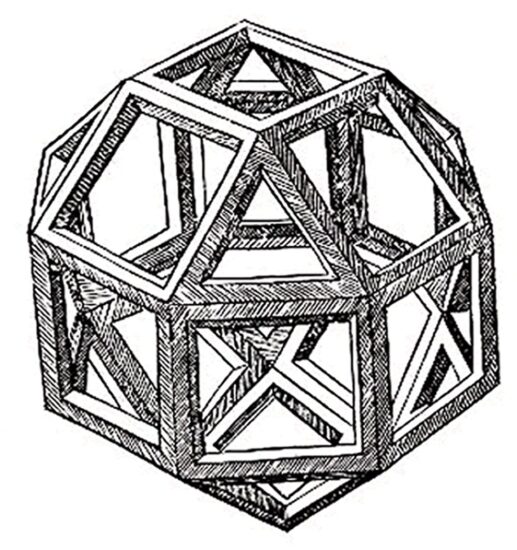
Il termine “divina proporzione” fu coniato solo nel 1509 dal matematico Luca Pacioli, autore del trattato De divina proportione, illustrato con i disegni dei solidi platonici realizzati da Leonardo da Vinci. Questo testo contribuì a diffondere la conoscenza del rapporto aureo tra artisti e architetti del Rinascimento, consacrandone il suo status quasi mitico.
Esempi di sezione aurea in natura
In natura la sezione aurea si manifesta con una frequenza sorprendente, suggerendo un modello di crescita efficiente ed ottimizzato. Ecco alcuni esempi documentabili:
- Fiori e piante: gran parte dei fiori ha un numero di petali che corrisponde a un numero della serie di Fibonacci (es. gigli 3, ranuncoli 5, delfini 8).
- Semi e infiorescenze: le infiorescenze sui girasoli seguono due serie di spirali che girano in senso orario e antiorario. Il numero di spirali in ciascuna direzione è quasi sempre una coppia di numeri di Fibonacci consecutivi (es. 34 e 55). Questo schema permette di impacchettare i semi nel modo più compatto possibile. Lo stesso avviene per le pigne e per la struttura dell’ananas.
- Fillotassi: la disposizione delle foglie su un ramo di un albero spesso segue la sequenza di Fibonacci per massimizzare l’esposizione alla luce solare di ogni foglia.
- Conchiglie e spirali: vari tipi di conchiglie, come quella del mollusco Nautilus, crescono seguendo una spirale logaritmica che è un’approssimazione perfetta della spirale aurea. Questa forma geometrica è data dai quarti di circonferenza inscritti in quadrati con lati equivalenti ai numeri della successione di Fibonacci.
- Alveari: in un alveare, il rapporto tra il numero di api femmine e quello dei maschi è spesso molto vicino a 1,618.

La divina proporzione nell’arte, musica e corpo umano
La presenza del numero della divina proporzione va oltre la biologia, toccando campi come l’arte, la musica e la fisica.
Arte e architettura
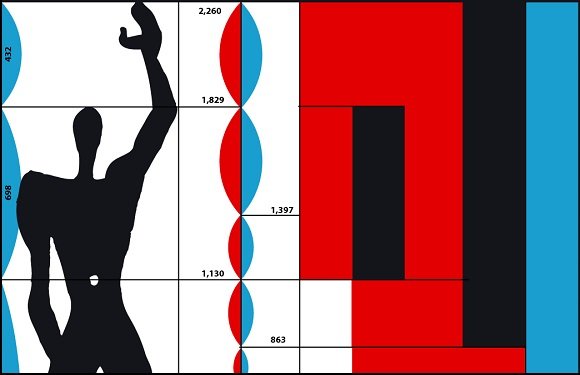
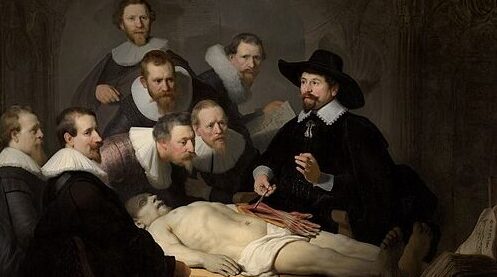
Secondo diverse teorie, molti artisti hanno fatto uso, consciamente o meno, della sezione aurea per creare opere percepite come armoniose. È il caso di Giotto, Cimabue, Leonardo da Vinci (basti pensare all’Uomo vitruviano o alla disposizione dei personaggi nell’Ultima cena) e Georges Seurat. In architettura, il caso più celebre è il Partenone di Atene, la cui facciata sarebbe inscritta in un rettangolo aureo. Sebbene alcuni studi moderni mettano in discussione l’intenzionalità di tale scelta, la correlazione dimensionale è notevole. Più recentemente, l’architetto Le Corbusier ha basato il suo sistema di proporzioni, il Modulor, proprio sulla sezione aurea e sulle misure del corpo umano. L’associazione con l’architetto ateniese Fidia, che supervisionò la costruzione del Partenone, è così forte che il numero Φ è anche chiamato “costante di Fidia”.
Un consiglio pratico per i fotografi: la “regola dei terzi” è una semplificazione del rapporto aureo. Posizionare i punti di interesse lungo queste linee o alle loro intersezioni può rendere una foto più dinamica ed equilibrata.
Musica e poesia
Nella musica troviamo il rapporto aureo in diverse forme. Il violino, in particolare quelli costruiti da maestri liutai come Stradivari, deve parte del suo suono eccezionale alla particolare forma della cassa armonica, le cui curve e proporzioni sembrano seguire la geometria aurea. Anche la struttura del pianoforte, con i suoi 13 tasti per ottava (8 bianchi e 5 neri, divisi in gruppi di 2 e 3), riflette la sequenza di Fibonacci. Già Pitagora aveva osservato che gli accordi musicali basati su rapporti di numeri interi piccoli risultassero particolarmente graditi all’orecchio umano. Molti compositori, da Mozart a Debussy, hanno strutturato le loro composizioni posizionando i climax o i cambi di tema in punti che dividono la durata totale del brano secondo il rapporto aureo.
In poesia, alcuni studi sull’Eneide di Virgilio hanno evidenziato come il rapporto tra le parti di dialogo e quelle di narrazione in certi libri si avvicini al rapporto Φ.
Anatomia umana
Il corpo umano stesso è una fonte di proporzioni auree. Sebbene con variazioni individuali, si possono riscontrare diverse corrispondenze:
- Il rapporto tra l’altezza di una persona e la distanza del suo ombelico da terra è spesso vicino a 1,618.
- Il rapporto tra la lunghezza del braccio (dalla spalla alla punta delle dita) e quella dell’avambraccio (dal gomito alla punta delle dita) si approssima al numero aureo.
- Anche le proporzioni della mano sono indicative: il rapporto tra le falangi del dito medio è un esempio di questa costante.
- A livello fisiologico, persino il ritmo cardiaco mostra questa proporzione: il rapporto tra la durata di una fase sistolica (contrazione) e una diastolica (rilassamento) in un cuore sano è approssimabile al rapporto aureo.
Applicazioni moderne nel design
Oggi, il rapporto aureo è uno strumento fondamentale nel mondo del design grafico e della progettazione di interfacce utente (ui/ux). Viene utilizzato per definire layout di pagine web, creare loghi (come quelli di Twitter e Pepsi) e stabilire gerarchie tipografiche armoniose. Utilizzare una griglia basata sulla sezione aurea aiuta a disporre gli elementi in modo bilanciato e naturale, guidando l’occhio dell’utente verso le informazioni più importanti.
| Ambito di applicazione | Esempio pratico |
|---|---|
| Web design | Definire la larghezza della colonna principale e della sidebar. Es: una pagina da 960px divisa in 593px e 367px. |
| Logo design | Costruire le proporzioni del logo usando cerchi e quadrati aurei per un risultato equilibrato. |
| Tipografia | Scegliere la dimensione del testo e dei titoli. Se il testo è 12px, il titolo potrebbe essere 12 * 1,618 = 19.4px (arrotondato a 19 o 20px). |
Psicologia ed estetica: il numero della bellezza?
La teoria più accreditata è quella per cui il phi sia alla base di ciò che il nostro cervello percepisce come “bello”, armonico ed efficiente. Questa preferenza innata potrebbe derivare dal fatto che riconosciamo inconsciamente questi schemi come segni di salute e di crescita naturale. È per questo motivo che la maggior parte degli studi riguardo questo numero sconfina nella psicologia e nell’estetica. Rimangono ancora molti dubbi e il dibattito è molto acceso, specialmente sulla reale intenzionalità del suo uso in opere antiche. Nulla di strano per un numero che è stato tanto affascinante da meritarsi il nome di proporzione divina.
Domande frequenti sul rapporto aureo (FAQ)
Come si calcola il numero aureo?
Il numero aureo (Φ) si può calcolare principalmente in due modi. Geometricamente, si ottiene quando il rapporto tra un segmento intero (a+b) e la sua parte maggiore (a) è uguale al rapporto tra la parte maggiore (a) e quella minore (b). Matematicamente, un modo semplice per approssimarlo è dividere un numero della successione di Fibonacci per il suo predecessore (es. 89 / 55 = 1,61818…).
Chi ha scoperto la sezione aurea?
La prima definizione scritta della sezione aurea risale al matematico greco Euclide nei suoi “Elementi” (circa 300 a.C.), anche se le sue proprietà erano probabilmente già note ai Pitagorici. Il termine “divina proporzione” è stato invece introdotto molto più tardi, nel 1509, da Luca Pacioli nel suo omonimo trattato.
Perché il rapporto aureo è così presente in natura?
Si ritiene che il rapporto aureo rappresenti un modello fondamentale di efficienza e crescita nel mondo naturale. Questa proporzione permette, ad esempio, di disporre i semi in un girasole o le foglie su un ramo nel modo più compatto e funzionale possibile, massimizzando l’esposizione alla luce o lo spazio disponibile. È un modello di ottimizzazione che la natura ha adottato in innumerevoli contesti.
Articolo aggiornato il: 28 gennaio 2026
Immagine dell’articolo sul rapporto aureo: Pixabay









One Comment on “Sezione aurea: definizione, valore del numero Phi ed esempi in natura”